Definitie:

Fie G = (V, E) un graf orientat. Se numeste retea de transport ansamblul R = (G, st, fin, c) unde

G este un graf orientat
st apartine lui V si d+(st) > 0, d-(st) = 0
fin apartine lui V si d-(st) > 0, d+(st) = 0, fin != st
c : V x V -> N, Daca [i, j] nu apartine lui E, atunci C(i,j) = 0

Exemple:

Mai jos puteti observa o retea de transport in care st este nodul 1, fin este nodul 7, iar valorile diferite de 0 ale functiei c sunt trecute pe arcuri:

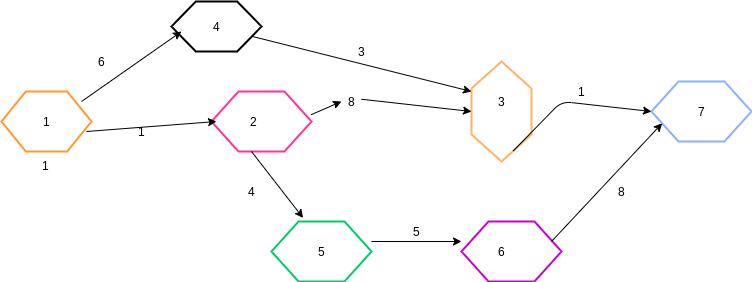
Semnificatie:

De la st la fin trebuie transportat ceva anume. Functia c are semnificatia de capacitate de transport intre oricare doua noduri.

O retea de transport se citeste dintr-un fisier text cu datele organizate ca mai jos:

Linia 1 n numarul de noduri Linia 2 - st and fin Urmatoarele linii sunt de forma i j c si au semnificatia ca de la nodul i de nodul j exista capacitatea de transport c.

7
1 7
1 2 1
2 3 8
3 7 1
1 4 5
4 3 3
2 5 4
5 6 5
7 7 8

Flux intr-o retea de transporta

Fie reteaua de transport R = (G, st, fin, c), unde G = (V, E) un graf orientat. Vom numi flux al retelei R, o functie q -> VxV -> N care indeplineste urmatoarele doua conditii:

pentru orice arc avem 0 <= q(i,j) <= c(i,j) adica fluxul nu poate depasi capacitatea arcului respectiv.
pentru orice varf din V, i apartine lui V - (st, fin) avem: Suma(q(i,j)) = Suma(q(j,i)) Acesta are seminificatia ca suma valorilor asociate prin q pentru arcele care ies din nodul i este egala cu suma valorilor asociate prin q pentru arcele care intra in i.

S = valoarea fluxului.

Determinarea fluxului de valoare maxima

Problema: Se da reteaua R = (G, st, fin, c) pe care este definit un flux q. Se cere un flux de valoare maxima pentru reteaua respectiva qMax.

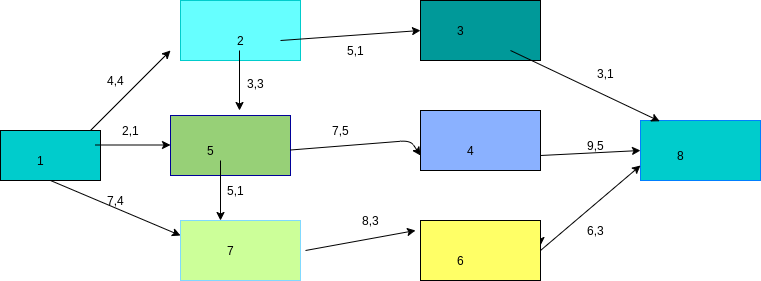
Pentru a intelege algoritmul trebuie sa insusim cateva notiuni. Exemplele vor fi date pe reteaua urmatoare in care st = 1 si fin = 8 si pentru care avem un flux q.

Fie un DRUM in reteaua R, de la st la fin, in care orice arc poate fi parcurs in sensul in care este orientat, fie in sens invers.

a) 1 2 3 8 in care toate arcele sunt parcurse in sensul pe care il au.
b) 1 5 7 6 8 in care arcul [5,7] este parcurs in sens invers. Celelalte arce sunt parcurse in sensul pe care il au.

Fiind dat un drum de la st la fin, fiecarui arc [i,j] care-l alcatuieste i se asociaza un numar numit valoare reziduala, in felul urmator:

*           c(i,j) - q(i,j), pentru [i,j] parcurs direct
* vr(i,j)
*           q(i,j) pentru [i, j] este parcurs invers.

exemplu: pentru drumul 1,5,7,6,8 avem:

* vr(1,5) = 2 - 1 = 1
* vr(5,7) = q(5,7)
* vr(7,6) = 8 - 3 = 5
* vr(6,8) = 6 -3 = 3

Se numeste drum in crestere in reteaua R, un drum de la st la fin in care orice arc poate fi parcurs, fie in sensul in care este dat, fie in sens invers si in care valoarea reziduala a fiecarui arc este diferita de 0.

a) 1 5 7 6 8 este un drum in crestere pentru ca este de la st la fin si valoarea reziduala a fiecarui arc este diferita de 0.
b) 1 2 3 8 nu este un drum in crestere pentru ca valoarea reziduala a arcului [1,2] = 0

Definim capacitatea reziduala a unui drum in crestere si o notam cu e, minimum valorilor reziduale ale arelor care alcatuiesc.

exemplu: pentru drumul in crestere 1 5 7 6 8 avem e = min(1,1,5,5) = 1

Criteriul de marire a fluxului: fiind dat un drum in crestere de capacitate reziduala e, modificam valorile determinate de q, pentru a obtine un flux de valoare mai mare astfel:

              q(i,j) daca [i,j] nu apartine drumului in crestere
* q'(i,j) =  q(i,j) + e , daca [i,j]  este parcurs in sens direct
             q(i,j) - e, daca [i,j] este parcurs in sens invers.

q'(1,5) = 1 + 1 = 2, q'(5,7) = 1 - 1 = 0, q'(7,6) = 3 + 1 = 4, q'(6,8) = 3 + 1 = 4             

q' > q

Pentru a gasi valoarea fluxului de valoare maxima suntem condusi la ideea de a gasi un drum in crestere si de a mari fluxul prin capacitatea sa reziduala, apoi sa gasim alt drum in crestere si sa marim din nou fluxul, pana cand nu mai avem drumuri in crestere. Atunci cand nu mai avem drumuri in crestere vom avea fluxul de valoare maxima. Un astfel de algoritm se incadreaza in strategia Greedy pentru ca la fiecare pas alege un drum in crestere si mareste valoarea functie pana la el, pana cand nu mai avem drumuri in crestere.

Bibliografie:

https://ocw.mit.edu/courses/6-046j-design-and-analysis-of-algorithms-spring-2012/7c2927794e61bd70c14c07728fa54375_MIT6_046JS12_lec13.pdf